NMPC with CasADi and Python – Part 3: State-space equations of a 2-DOF robot with SymPy or MATLAB
CasADi is a powerful open-source tool for nonlinear optimization. It can be used with MATLAB/Octave, Python, or C++, with the bulk of the available resources referencing the former two options. This post series is intended to show a possible method of developing a simulation for an example system controlled by Nonlinear Model Predictive Control (NMPC) using CasADi and Python.
In this post, we will look at determining the system equations of a robot with two degrees of freedom in stace-space form. These state-space equations can be used for simulation and for developing a nonlinear model predictive controller. For some transformation tasks, Python with SymPy will be utilized and an alternative using the MATLAB Symbolic Math Toolbox will be shown.
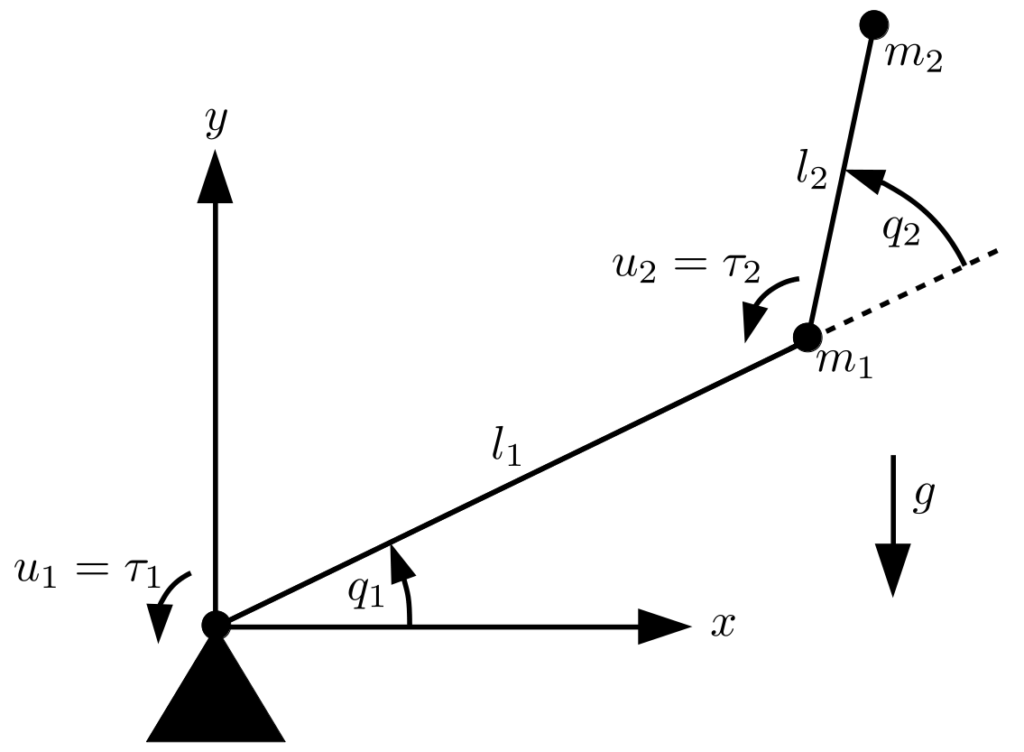
During the following, we are considering a robot with two links, two masses at the end of the links, and motors applying torque as control input at the joints. A diagram of the robot is shown below.
NMPC with CasADi and Python – Part 2: Simulation of an uncontrolled system
CasADi is a powerful open-source tool for nonlinear optimization. It can be used with MATLAB/Octave, Python, or C++, with the bulk of the available resources referencing the former two options. This post series is intended to show a possible method of developing a simulation for an example system controlled by Nonlinear Model Predictive Control (NMPC) using CasADi and Python.
In this post, we will try to simulate an uncontrolled system with a forward Euler and a 4th order Runge-Kutta integration method. The latter can be the base for future closed-loop simulations.