Efficient Union-Find in C++ – or: Disjoint-set forests with Path Compression and Ranks

tl;dr: https://github.com/nspo/graphs-cpp/blob/master/general/include/DisjointSets.h

Basics

Disjoint-set data structures are useful in cases where you have a (possibly very large) number of elements and want to repeatedly execute two operations: marking two elements as connected, and checking whether two elements are connected. A query of the latter kind does not necessarily mean that the two elements p and q were explicitly connected to each other by the caller – it is possible, e.g., that p was first connected to the element r, and only much later in time q was also connected to r.

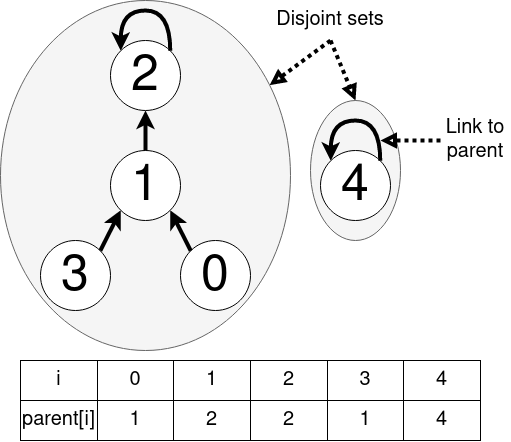
The disjoint sets in the data structure are commonly represented by trees, where each node in the tree contains a link to its parent, the parent in turn contains a link to the parent’s parent, and so on. The node at the root of the tree contains contains a link to itself, i.e. it is its own parent. All nodes of a tree are in the same set. It can be easily checked whether two elements are in the same set by evaluating whether they have the same root. The set of trees is called the disjoint-set forest. While this approach is common and can be implemented efficiently, the C++ standard library does not contain an implementation – this post tries to offer one.

Let us assume the data structure is used for N elements, each having an index between 0 and N-1. The links to the parent nodes of all elements can then easily be saved in an array of length N. If parent[p] == q, then q is the parent of p. Whenever two sets containing the elements p and q should be merged, this can be achieved by attaching the root of one element to the root of the other.

Public interface

The interface of the class DisjointSets is simple. The constructor takes a number of elements N and creates N disjoint sets:

DisjointSets disjointSets(20);

Each element can then be referenced with an index between 0 and N-1. To connect the two sets containing elements p and q, you execute:

disjointSets.setUnion(p, q);

To check whether p and q are in the same set:

if (disjointSets.connected(p, q)) { // ...

Additionally, the C++ code contains a public size() function which returns the number of elements (not the number of disjoint sets).

Necessary optimizations

To ensure fast access and that the implicit trees do not become too high, two optimizations are necessary (though the details can vary): considering the size of the subtrees when joining two sets (using ranks or weights), and making sure that we flatten a tree whenever we step through it (using path compression or path halving).

Union by rank

The rank of a node is a heuristic used when joining two sets. It is an upper bound on the height of the node, which means an upper bound on the number of edges that would have to be crossed to go downwards until a leaf is reached. If a node p has rank 1, there will be either zero or one layer of nodes below it which have p as their parent. No nodes will have a node in the (potential) layer below p as their parent. The initial rank of a node which is not connected to any other node is 0. When the sets containing two nodes p and q are to be joined, the roots of both must be identified (say rp and rq respectively). For the next step, there are two possibilities:

1. If one root (say rp) has a lower rank than the other one (rq), then rq is set as the parent of rp. The ranks do not change. This is intended to avoid attaching subtrees with a high number of nodes below them to a node with a lower height.
2. If both roots have equal rank, then one root is arbitrarily chosen as parent and its rank is increased by 1.

Path compression

One central private method of the implementation will be findRoot, which will return the root element for a given input element. As mentioned above, it is beneficial to have trees with a low height. If that is the case, the root of each element can be found quickly. The ideal situation would be if all nodes which are not root nodes would point directly to their root. Path compression is a simple technique that tries to get close to this: each time a path from some kind of node to a root is traversed, the structure is modified so that the traversed nodes point directly to the root. Using recursion, this can be achieved with minimal extra code.

Time complexity

The two aforementioned optimizations lead to operations being possible in nearly constant amortized time. Actually, the time complexity depends on number of union operations and grows with the inverse of the Ackermann function – but the result of this inverse is smaller than or equal to 4 for any reasonable input.

Code

The source code is available as an independent, header-only class in my Github repository related to weighted graphs (as this data structure is helpful e.g. for identifying a Minimum Spanning Tree of a weighted graph):

https://github.com/nspo/graphs-cpp/blob/master/general/include/DisjointSets.h

References

Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Data Structures for Disjoint Sets. In Introduction to algorithms. Cambridge (Inglaterra): Mit Press.